Equation of a circle in various forms:
General equation of a circle:


General equation of a circle:
centre is 
radius is 
(i)circle with centre at  and radius
and radius  is:
is:
(ii)circle with end points of diameter are given as  and
and  :
:
(iii)circle passing through three points  ,
,  ,
, :
:
Equations of tangent:
(i)Slope form: the equation of a tangent of slope m to the circle  is
is
The coordinates of points of contact
(ii)Point form: the equation of the tangent at point  to circle
to circle
Pair of tangents from point  to
to 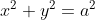 :
:
Length of tangents from  to
to  :
:
Normal to a circle:
The normal at any point is a straight line perpendicular to the tangent at that point.
chord of contact:
the equation of the chord of contact of tangents drawn from a point P to the circle
to the circle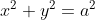 is
is
Parametric equations of a circle:
is the required parametric equation of the circle
intersection of a circle with a straight line:
Let the circle  and the line
and the line 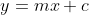 substituting value of y
substituting value of y
Angle of intersection of two circles:
circles passing through the intersection point of a given circle and a given line:
equation of a circle through the points of intersection of two circles :

No comments:
Post a Comment