Domain:

The domain of y=f(x) is set of all real x for which f(x) is defined(real).

Range(co-domain):

The range of y=f(x) is collection of all outputs f(x) corresponding to each real number in the domain.

MAPPING OF FUNCTION

Maps are a convenient way to visualise functions, or more generally, the association between two sets.

A map relates one set to another using some rule.

For example, $y = f(x) = {x^2}$ , $A = \{1, 2, 3, 4\},$ $B = \{1,4,9,16\}$

Domain Range

Kinds of function

one-one-onto bijective(injective & surjective)
one-one-into only injective not surjective
many-one-onto not injective only surjective
many-one-into neither injective nor surjective

one-one mapping:If f(x)=f(y) => x=y i.e for $f:A\rightarrow B$ different elements of A has different images in B.otherwise many to one

into function:For $f:A\rightarrow B$ if there exists an element in B having no pre image in A.

onto function: For $f:A\rightarrow B$ such that each element of B is the f image of at least one element in A

absolute value function

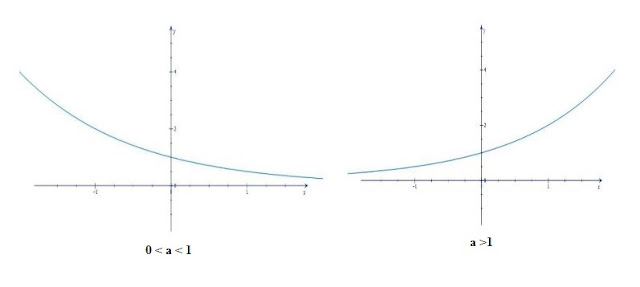
$y=\left | x \right |=\left\{\begin{matrix} x, \ x\geq 0\\ -x, \ x< 0 \end{matrix}\right.$

exponential function

$f\left ( x \right )=a^{x} \ ,a> 0,a\neq 1$

Domain = real number, Range ] $0,\infty$ [

logarithmic function

$f\left ( x \right )=\log_{a} x \ \ ; \ x,a> 0 \ & \ a\neq 1$

Polynomial function

$f\left ( x \right )=a_{0}+a_{1}x+.....+a_{n}x^{n}$

n is non negative integer

characteristics function

$\chi_{A}\left ( x \right )=\left\{\begin{matrix} 1, \ x\in A\\ o, \ x\notin A \end{matrix}\right.$

used in probability theory

signum function

$y=sgn\left ( x \right )=\left\{\begin{matrix} \frac{\left | x \right |}{x}, \ x\neq 0\\ 0 \ , \ x=0 \end{matrix}\right.=\left\{\begin{matrix} 1 \ , x> 0\\ -1 \ , x< 0\\ 0 \ , x= 0 \end{matrix}\right.$

greatest integer function

if $n\leq x< n + 1$

then

$\left [ x \right ]=n$

where $\left [ x \right ]$ is greatest integer function

similarly least integer function

composite function

Let us consider two function $f:X\rightarrow Y_{1}$ and $g:Y_{1}\rightarrow Y$

we define $h:X\rightarrow Y$ such that

$h\left ( x \right )=g\left ( f\left ( x \right ) \right )=\left ( gof \right )\left ( x \right )$

Trigonometric functions

There are six basic trigonometric functions

sine : $R\rightarrow \left [ -1,1 \right ]$

cosine : $R\rightarrow \left [ -1,1 \right ]$

tangent : $R'\rightarrow R \ where \ R'=R-\left \{\left ( 2n+1 \right )\frac{\Pi }{2} \ :n\in Z \right \}$

cotangent : $R''\rightarrow R \ where \ R''=R-\left \{n\Pi \ :n\in Z \right \}$

secant : $R'\rightarrow R$

cosecant : $R''\rightarrow R$

Click here for more details

properties of function

Even and Odd Functions

A function is even if $f(x) = f( - x)$

A function is odd if $f(x) = - f( - x)$

Periodic Functions

A function f(x) is said to be periodic if

$f\left ( x+T \right )=f\left ( x\right ), \ \forall \ x\in R$

T is the period

A function 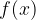$f(x)$ is increasing if $f$ increases as $x$ increases.

A function 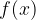$f(x)$ is decreasing if $f$ decreases as $x$ increases.

Inverse of Function

The inverse of a function 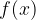$f(x)$ is a function $g(x)$ such that if $f$ maps an element ‘ $a$ ’ to an element ‘ $b$ ’, $g$ maps ‘ $b$ ’ to ‘ $a$ ’.

In more formal terms, $g(f(x)) = x$ . That is, $g$ reverses the action of $f$ on $x$ .

For a function to be invertible, it should be one-one and onto (also called a bijective function).

e.g.

ELECTRICAL ENGINEERING
ENGINEERING MATHEMATICS	Electric Circuits and Fields
Signals and Systems	Electrical Machines
Power Systems	Control Systems
Electrical and Electronic Measurements	Power Electronics and Drives
Analog Electronics	Digital Electronics

Functions

Even and Odd Functions

Periodic Functions

No comments:

Post a Comment