SHORT NOTES: Vectors

Scalars only magnitude.Ex: Distance,Temperature, speed, mass

Vectors both magnitude and direction. The magnitude of $\vec{v}$ is written $\left |\vec{v} \right |\equiv v$ .Ex: displacement, velocity, acceleration and force

Unit Vector: only give direction i.e vector with magnitude "one".

Ex: $\frac{\vec{v}}{v}=\hat{v}$ (unit vector)

Note: $\hat{i},\hat{j},\hat{k}$ are unit vectors along x,y,z axis.

Vectors are equal if they have the same magnitude and direction.

The negative of a vector has the same magnitude but opposite direction.

Scalar multiplication:Multiplication or division of a vector by a scalar results in a vector for which

(a)only the magnitude changes if the scalar is positive

(b)the magnitude changes and the direction is reversed if the scalar is negative.

The projections of a vector along the axes of a rectangular co-ordinate system are called the components of the vector.

$\vec{A}=A_x\hat{i}+A_y\hat{j}$

Similarly for 3D i.e for x,y,z axis.

Addition of vectors:

1.To add vectors by components $\vec{R}=\vec{A}+\vec{B}$

Find $R_x=A_x+B_X$ and $R_y=A_y+B_y$ .

Then $\left |\vec{R} \right |={\sqrt{R_x^2+R_y^2}}$ and $\theta =\tan^{-1}\frac{R_y}{R_x}$

2.Triangle Law: $R^2=A^2+B^2+2AB\cos \theta$ and $\tan \beta =\frac{B\sin \theta}{A+B\cos \theta}$

$\theta$ is angle between A and B vector i.e by how much angle the vector B rotates/shift from the direction of vector A in anti-clockwise direction.

$\beta$ is angle between A and R vector

3.Parallelogram: Same formula as triangle law

Subtraction of a vector is defined by adding a negative vector.

Dot Product:

$\vec{A}.\vec{B}=AB\cos \theta$ Given A , B , $\theta$ are known

$\vec{A}.\vec{B}=A_xB_x+A_yB_y+A_zB_z$ If A,B are expressed in compent form

Note: $\theta=\cos^{-1}\frac{A_xB_x+A_yB_y+A_zB_z}{AB}$ A,B are magnitude

Geometrical interpretations: $\vec{A}.\vec{B}=AB\cos \theta$ $=A\cos \theta X B$ = Projection of A on B

Cross products:

$\vec{A}x\vec{B}=AB\sin \theta\hat{n}$ where $\hat{n}$ is the normal to the plane containing A & B with direction defined by thumb rule or screw rule

$\vec{A}x\vec{B}=\begin{vmatrix} \hat{i} &\hat{j} &\hat{k} \\A_X &A_y &A_z \\B_x &B_y &B_z \end{vmatrix}$

Note:

$\begin{align} \mathbf{i}&=\mathbf{j}\times\mathbf{k}\\ \mathbf{j}&=\mathbf{k}\times\mathbf{i}\\ \mathbf{k}&=\mathbf{i}\times\mathbf{j} \end{align}$ $\begin{align} \mathbf{k\times j}=&-\mathbf{i}\\ \mathbf{i\times k}=&-\mathbf{j}\\ \mathbf{j\times i}=&-\mathbf{k} \end{align}$ $\mathbf{i}\times\mathbf{i}=\mathbf{j}\times\mathbf{j}=\mathbf{k}\times\mathbf{k}=\mathbf{0}$

Geometrical interpretations:

The magnitude of the cross product can be interpreted as the positive area of the parallelogram having a and b as sides

$A = \left\| \mathbf{a} \times \mathbf{b} \right\| = \left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \sin \theta. \,\!$

Similarly Area of triangle is half of cross product.

Scalar triple products:

The scalar triple product of three vectors A, B, and C is denoted [A,B,C] and defined by

Geometric interpretation:

Geometrically, the scalar triple product

$\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})$

is the (signed) volume of the parallelepiped

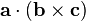
$\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c}) = \det \begin{bmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \\ \end{bmatrix}.$

ELECTRICAL ENGINEERING
ENGINEERING MATHEMATICS	Electric Circuits and Fields
Signals and Systems	Electrical Machines
Power Systems	Control Systems
Electrical and Electronic Measurements	Power Electronics and Drives
Analog Electronics	Digital Electronics

Vectors

Geometric interpretation:

No comments:

Post a Comment