A limit is the value that a function or sequence "approaches" as the input or index approaches some value
Suppose f is a real-valued function and c is a real number. The expression
means that f(x) can be made to be as close to L as desired by making x sufficiently close to c. In that case, the above equation can be read as "the limit of f of x, as x approaches c, is L".
For example 

Left hand and right hand limit of a function
|
e.g.
Sgn is signum function
The limit of
&
Limits of the form
Algebra of Limits Let
Sandwich theorem:
If
for all x in neighborhood of a then
Existence of limit at Methods for Evaluation of Limits
(A) DIRECT SUBSTITUTION:
(B) FACTORIZATION:
(C) RATIONALIZATION:
(D) REDUCTION TO STANDARD FORMS:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
(ix)
(E)Using L'Hospital rule:
If f(x) and g(x) are continuous and differentiable at x=a,
&
we can repeat this process till limit is evaluated
(F)Evaluation of left hand and right hand limit:
RHL of
A function f(x) is said to be continuous at x=a if
i.e LHL=RHL=value of function at x=a
Differentiability of a function at a point:
f(x) ,defined in (a,b), is said to be differentiable at x=c where iff i.e. Relationship between continuity and differentiability
|

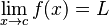
No comments:
Post a Comment