A rectangular array of 'mn' numbers in the form of m rows and n columns is called matrix of order
m by n written as m x n matrix

Two matrices A and B are equal if they are of same order and all corresponding elements are equal.
Addition of Matrices:
![A \pm B = \left[ {{a_{ij}}} \right]\; \pm \;\left[ {{b_{ij}}} \right] A \pm B = \left[ {{a_{ij}}} \right]\; \pm \;\left[ {{b_{ij}}} \right]](http://s.wordpress.com/latex.php?latex=A%20%5Cpm%20B%20%3D%20%5Cleft%5B%20%7B%7Ba_%7Bij%7D%7D%7D%20%5Cright%5D%5C%3B%20%5Cpm%20%5C%3B%5Cleft%5B%20%7B%7Bb_%7Bij%7D%7D%7D%20%5Cright%5D&bg=T&fg=000000&s=1)
For example
![\left[ {\;\begin{array}{*{20}{c}} 1&{ - 2}\\ 3&{\;\;4}\\ 5&{ - 3} \end{array}\;} \right]\;\; + \;\;\left[ {\begin{array}{*{20}{c}} {\;\;2}&{\;1}\\ { - 1}&{\;3}\\ {\;\;4}&{\;2} \end{array}\;} \right]\;\; = \;\left[ {\;\begin{array}{*{20}{c}} 3&{\; - 1}\\ 2&{\;\;\;7}\\ 9&{\; - 1} \end{array}\;} \right]\; \left[ {\;\begin{array}{*{20}{c}} 1&{ - 2}\\ 3&{\;\;4}\\ 5&{ - 3} \end{array}\;} \right]\;\; + \;\;\left[ {\begin{array}{*{20}{c}} {\;\;2}&{\;1}\\ { - 1}&{\;3}\\ {\;\;4}&{\;2} \end{array}\;} \right]\;\; = \;\left[ {\;\begin{array}{*{20}{c}} 3&{\; - 1}\\ 2&{\;\;\;7}\\ 9&{\; - 1} \end{array}\;} \right]\;](http://s.wordpress.com/latex.php?latex=%5Cleft%5B%20%7B%5C%3B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D%20%201%26%7B%20-%202%7D%5C%5C%20%203%26%7B%5C%3B%5C%3B4%7D%5C%5C%20%205%26%7B%20-%203%7D%20%20%5Cend%7Barray%7D%5C%3B%7D%20%5Cright%5D%5C%3B%5C%3B%20%2B%20%5C%3B%5C%3B%5Cleft%5B%20%7B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D%20%20%7B%5C%3B%5C%3B2%7D%26%7B%5C%3B1%7D%5C%5C%20%20%7B%20-%201%7D%26%7B%5C%3B3%7D%5C%5C%20%20%7B%5C%3B%5C%3B4%7D%26%7B%5C%3B2%7D%20%20%5Cend%7Barray%7D%5C%3B%7D%20%5Cright%5D%5C%3B%5C%3B%20%3D%20%5C%3B%5Cleft%5B%20%7B%5C%3B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D%20%203%26%7B%5C%3B%20-%201%7D%5C%5C%20%202%26%7B%5C%3B%5C%3B%5C%3B7%7D%5C%5C%20%209%26%7B%5C%3B%20-%201%7D%20%20%5Cend%7Barray%7D%5C%3B%7D%20%5Cright%5D%5C%3B&bg=T&fg=000000&s=1)
Example




![A = \left[ {\;\begin{array}{*{20}{c}} 2&4\\ 1&1\\ 3&7 \end{array}\;} \right] \,\,\,\,\,\,\, \Rightarrow \,\,\,\, {A^T} = \left[ {\;\begin{array}{*{20}{c}} 2&1&3\\ 4&1&7 \end{array}\;} \right] A = \left[ {\;\begin{array}{*{20}{c}} 2&4\\ 1&1\\ 3&7 \end{array}\;} \right] \,\,\,\,\,\,\, \Rightarrow \,\,\,\, {A^T} = \left[ {\;\begin{array}{*{20}{c}} 2&1&3\\ 4&1&7 \end{array}\;} \right]](http://s.wordpress.com/latex.php?latex=A%20%3D%20%5Cleft%5B%20%7B%5C%3B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D%20%202%264%5C%5C%20%201%261%5C%5C%20%203%267%20%20%5Cend%7Barray%7D%5C%3B%7D%20%5Cright%5D%20%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%20%20%5CRightarrow%20%20%5C%2C%5C%2C%5C%2C%5C%2C%20%7BA%5ET%7D%20%3D%20%5Cleft%5B%20%7B%5C%3B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D%20%202%261%263%5C%5C%20%204%261%267%20%20%5Cend%7Barray%7D%5C%3B%7D%20%5Cright%5D&bg=T&fg=000000&s=1)








 that element which is in the
that element which is in the  row and
row and  column
column

 is called minor of
is called minor of  which is calculated by taking the determinant of matrix formed by
which is calculated by taking the determinant of matrix formed by

![A = \left[ {\;\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}}\\ {{a_4}}&{{a_5}}&{{a_6}}\\ {{a_7}}&{{a_8}}&{{a_9}} \end{array}\;} \right] A = \left[ {\;\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}}\\ {{a_4}}&{{a_5}}&{{a_6}}\\ {{a_7}}&{{a_8}}&{{a_9}} \end{array}\;} \right]](http://s.wordpress.com/latex.php?latex=A%20%3D%20%5Cleft%5B%20%7B%5C%3B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D%20%20%7B%7Ba_1%7D%7D%26%7B%7Ba_2%7D%7D%26%7B%7Ba_3%7D%7D%5C%5C%20%20%7B%7Ba_4%7D%7D%26%7B%7Ba_5%7D%7D%26%7B%7Ba_6%7D%7D%5C%5C%20%20%7B%7Ba_7%7D%7D%26%7B%7Ba_8%7D%7D%26%7B%7Ba_9%7D%7D%20%20%5Cend%7Barray%7D%5C%3B%7D%20%5Cright%5D&bg=T&fg=000000&s=1) with corresponding co-factors
with corresponding co-factors
![\widetilde A = \left[ {\;\begin{array}{*{20}{c}} {{C_1}}&{{C_4}}&{{C_7}}\\ {{C_2}}&{{C_5}}&{{C_8}}\\ {{C_3}}&{{C_6}}&{{C_9}} \end{array}\;} \right] \widetilde A = \left[ {\;\begin{array}{*{20}{c}} {{C_1}}&{{C_4}}&{{C_7}}\\ {{C_2}}&{{C_5}}&{{C_8}}\\ {{C_3}}&{{C_6}}&{{C_9}} \end{array}\;} \right]](http://s.wordpress.com/latex.php?latex=%5Cwidetilde%20A%20%3D%20%5Cleft%5B%20%7B%5C%3B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D%20%20%7B%7BC_1%7D%7D%26%7B%7BC_4%7D%7D%26%7B%7BC_7%7D%7D%5C%5C%20%20%7B%7BC_2%7D%7D%26%7B%7BC_5%7D%7D%26%7B%7BC_8%7D%7D%5C%5C%20%20%7B%7BC_3%7D%7D%26%7B%7BC_6%7D%7D%26%7B%7BC_9%7D%7D%20%20%5Cend%7Barray%7D%5C%3B%7D%20%5Cright%5D&bg=T&fg=000000&s=1) Adjoint of A=Transpose of cofactor matrix
Adjoint of A=Transpose of cofactor matrix


![\left[ {\;\begin{array}{*{20}{c}} 1&0&0\\ 0&{ - 1}&0\\ 0&0&2 \end{array}\;} \right] \left[ {\;\begin{array}{*{20}{c}} 1&0&0\\ 0&{ - 1}&0\\ 0&0&2 \end{array}\;} \right]](http://s.wordpress.com/latex.php?latex=%5Cleft%5B%20%7B%5C%3B%5Cbegin%7Barray%7D%7B%2A%7B20%7D%7Bc%7D%7D%20%201%260%260%5C%5C%20%200%26%7B%20-%201%7D%260%5C%5C%20%200%260%262%20%20%5Cend%7Barray%7D%5C%3B%7D%20%5Cright%5D&bg=T&fg=000000&s=1)
 i.e
i.e 

 i.e
i.e 




m by n written as m x n matrix
Equality of matrices:
Two matrices A and B are equal if they are of same order and all corresponding elements are equal.
Addition of Matrices:
For example
Multiplication by a scalar:
If we multiply a matrix ![A = [{a_{ij}}] A = [{a_{ij}}]](http://s.wordpress.com/latex.php?latex=A%20%3D%20%5B%7Ba_%7Bij%7D%7D%5D&bg=T&fg=000000&s=1) by
by  we get the matrix
we get the matrix ![\lambda A = [\lambda {a_{ij}}].\; \lambda A = [\lambda {a_{ij}}].\;](http://s.wordpress.com/latex.php?latex=%5Clambda%20A%20%3D%20%5B%5Clambda%20%7Ba_%7Bij%7D%7D%5D.%5C%3B&bg=T&fg=000000&s=1)
Example
Multiplication Of Matrices:
To obtain the element  of
of  , we multiply
, we multiply  of
of 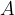 with
with  of
of  :
:

To obtain the element  of
of  we multiply
we multiply  of
of  with
with  of
of  :
:

To obtain the element  of
of  we multiply
we multiply  of
of 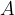 with
with  of
of  :
:

Proceeding this way, we obtain all the elements of  .
.
If 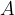 is or order
is or order  , and
, and  of order
of order  , then to obtain the element
, then to obtain the element  in
in  , we multiply
, we multiply  in
in 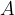 with
with  in
in  :
:

Transpose:
Note:-  ,
,
Determinant of Matrices:
Each  will have its corresponding co-factor
will have its corresponding co-factor 
eleminating the 'i' row and 'j' column.
For example minor of  is
is 
Properties of determinant:
- The value of determinant is not changed when rows are changed into columns and columns into rows.
- If any two rows or columns of a determinant are interchanged, the sign of the determinant changes but its magnitude remains the same
- A determinant having two rows or two columns identical has the value zero
- Multiplying all the elements of a row (or column) by a scalar (a real number) is equivalent to multiplying the determinant by that scalar
- A determinant can be split into a sum of two determinants along any row or column
Order two :
Order three :
Note:
Diagonal matrix
All non-diagonal elements are zero.
Symmetric matrix:
Skew Symmetric Matrix:
Main diagonal elements are zero
Solutions of simultaneous linear equations:
1.Cramer's rule:
Consider a system






-
consistent and unique solution
and at least one of
is non zero-Inconsistent and no solution
infinitely many solution
2.Matrix method:
,

No comments:
Post a Comment