SHORT NOTES: Complex Numbers

$N\subset W\subset Z\subset Q\subset R$

Natural no.(N) ,Whole no.(W) , Integers(Z or I) , Rational(Q) & Irrational no.(Q'), Real no(R).

Imaginary Number is square root of a negative real number e.g.

$x^2+1=0\Rightarrow x=\pm \sqrt{-1}$

which is imaginary.so the quantity 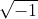$\sqrt{-1}$ is denoted by $i$ .Thus $i=\sqrt{-1}$

$i^n=(-1)^\frac{n}{2}$ if n is even

$i^n=(-1)^\frac{n-1}{2}$ if n i odd

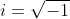
Complex Number: 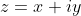$z=x+iy$ = Re z + i Im z

Algebra of complex numbers:

$a+ib=c+id\Rightarrow a=c,b=d$

$(a+ib)+(c+id)=(a+c)+i(b+d)$ Addition

$(a+ib)(c+id)=(ac-bd)+i(ad+bc)$ Multiplication

$\overline{a+ib}=a-ib$ Conjugation

Polar representation:

$a=rcos\theta , b=rsin\theta\\z=a+ib=r(cos\theta+isin\theta)$

Modulus of a complex number:

$\left | z \right |=\sqrt{(x^2+y^2)}$

Properties of modulus:

Hint: The above property can be remembered by thinking 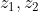$z_1,z_2$ as two sides of a triangle so that third side which is resultant of 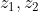$z_1,z_2$ is always less than equal to sum of individual side and always greater than equal to difference of two sides which is basic theorem of triangle.

Principal argument:

$Arg(z)=\theta=tan^{-1}\frac{b}{a}$

The value of $\theta$ where $-\pi< \theta< \pi$ is called principle argument.

Euler's notation:

$z=re^{i\theta}=r(cos\theta+isin\theta)$

cube roots of unity:

$x=\sqrt[3]{1}\Rightarrow x=1,\frac{-1+i\sqrt{3}}{2},\frac{-1-i\sqrt{3}}{2}\Rightarrow x=1,\omega,\omega^2$

properties of 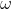$\omega$ :

$\omega^{3r}=1,\omega^{3r+1}=\omega,\omega^{3r+2}=\omega^2\\$

$1+\omega^r+\omega^{2r}=o$ if 'r' is not multiple of '3'

$1+\omega^r+\omega^{2r}=3$ if 'r' is multiple of '3'

Geometrical interpretation:

$\left | z-z_0 \right |=a$ circumference of a circle with center $z_0$ and radius a

$\left | \frac{z-z_1}{z-z_2} \right |=k$ Circle if $k\neq 1$

perpendicular bisector if 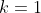$k=1$

Logarithm of complex no.

$\log z=\log (re^{i(\theta+2n\pi ))})=\log r+i(\theta+2n\pi)=\log\left | z \right |+iArgz+2n\pi$

if we put n=0 we get principle value of log z.

ELECTRICAL ENGINEERING
ENGINEERING MATHEMATICS	Electric Circuits and Fields
Signals and Systems	Electrical Machines
Power Systems	Control Systems
Electrical and Electronic Measurements	Power Electronics and Drives
Analog Electronics	Digital Electronics

Complex Numbers

No comments:

Post a Comment